
In primis, nel rinviare all’articolo LA MOLTIPLICAZIONE FRA IL TASSO E IL DEBITO RESIDUO DEL SISTEMA FRANCESE È NEL REGIME COMPOSTO ANCHE NEL PREAMMORTAMENTO DOVE LE QUOTE CAPITALI SONO PARI A ZERO e all’articolo GLI INTERMEDIARI CON IL SISTEMA FRANCESE CONOSCONO PERFETTAMENTE LE REGOLE MATEMATICHE E GIURIDICHE: BANCA IFIS USA IL TASSO PERIODALE EQUIVALENTE DEL REGIME COMPOSTO SIA NEL PREAMMORTAMENTO FINANZIARIO SIA NELL’AMMORTAMENTO, la tesi di chi sostiene che l’ammortamento ITALIANO comporta l’applicazione del REGIME SEMPLICE (si veda sia le conclusioni dei Sostituti Procuratori Generali della Cassazione Anna Maria Soldi e Stanislao De Matteis nell’articolo MEMORIA EX ART. 378 C.P.C. DEL PUBBLICO MINISTERO DELLA CASSAZIONE DEL 06-02-2024 (SU RINVIO PREGIUDIZIALE DI SALERNO DEL 19-07-2023 N. 9585) sia la conclusione più rilevante di tutto il rapporto AMASES di pagina 21 che afferma che “se vale la regola di calcolo degli interessi su espressa (formalizzata nella Reg. 1 del rapporto a pagina 17), una sequenza input di quote capitale tutte positive (o almeno non negative) è garanzia di assenza di interessi su interessi in ogni stadio del PAST” nell’articolo COMMISSIONE A.M.A.S.E.S SULL’ANATOCISMO: LA MISTIFICAZIONE DELLA VERITÀ MATEMATICA UTILIZZANDO LA NORMATIVA) è in palese contraddizione con l’impianto teorico di base della matematica finanziaria così come espresso, ad esempio, nei manuali sia del Prof. ALESSANDRO CASANO (Elementi di Algebra, Palermo, 1845) sia del Prof. EUGENIO LEVI (Corso di Matematica Finanziaria, La Goliardica Milano,1953) sia del Prof. GIUSEPPE OTTAVIANI (Lezioni di Matematica Finanziaria, Veschi, Milano, 1988) e, cioè, è in palese contraddizione con l’impianto teorico che afferma che se gli interessi che maturano in ogni singolo periodo sono calcolati moltiplicando il tasso effettivo annuo (o il tasso periodale effettivo o il tasso periodale NON equivalente perché semplicemente determinato dividendo il TAN per il tipo di periodicità adottato) per il DEBITO RESIDUO non ancora rimborsato del PDA “FRANCESE” o del PDA “ITALIANO“, questa assunzione implica che è il regime dell’INTERESSE COMPOSTO a regolare il contratto.
Infatti, nel rinviare all’articolo BONFERRONI 1937 QUALSIASI PRESTITO GRADUALE PUÒ ESSERE TRASFORMATO IN MANIERA EQUIVALENTE IN UNA SOMMA DI PRESTITI ELEMENTARI e all’articolo IL BULLET È ANATOCISTICO, in tutti i manuali di matematica storici rintracciabili solo nelle biblioteche universitarie perché non più in commercio (quello del 1845 del Prof. ALESSANDRO CASANO, quello del 1937 del Prof. CARLO BONFERRONI, quelli del 1953 e 1964 del Prof. EUGENIO LEVI, quello del 1983 del Prof. GIUSEPPE VAROLI, quello del 1988 del Prof. GIUSEPPE OTTAVIANI, quello del 1994 del Prof. FRANCO MORICONI) si afferma in maniera inequivocabile che l’ammortamento ITALIANO è regolato dal REGIME COMPOSTO degli interessi.
Non solo, si evidenzia che sul sito della Cassazione del Convegno 31 gennaio 2024 : Mutuo bancario con ammortamento alla francese (dove il Sostituto Procuratore Generale Stanislao De Matteis è stato il coordinatore del convegno) è pubblicata la slide del Prof. CARLO MARI denominata la “MATEMATICA VIOLATA” dove si dimostra che sia nell’ammortamento alla FRANCESE sia nell’ammortamento all’ITALIANA è applicato il REGIME COMPOSTO così come illustrato dall’impianto teorico di base della matematica finanziaria (il Prof. CARLO MARI cita nel suo scritto i manuali storici sia del Prof. ALESSANDRO CASANO (Elementi di Algebra, Palermo, 1845) sia del Prof. GIUSEPPE OTTAVIANI (Lezioni di Matematica Finanziaria, Veschi, Milano, 1988) contestando apertamente la conclusione più rilevante di tutto il rapporto AMASES di pagina 21 che afferma che “se vale la regola di calcolo degli interessi su espressa (formalizzata nella Reg. 1 del rapporto a pagina 17), una sequenza input di quote capitale tutte positive (o almeno non negative) è garanzia di assenza di interessi su interessi in ogni stadio del PAST“).
In altre parole, la slide del Prof. CARLO MARI dimostra la balla matematica che i c.d. “PAST AMASES” a rata costante (AMMORTAMENTO FRANCESE) e i c.d. “PAST AMASES” con quote di capitale costanti (AMMORTAMENTO ITALIANO) soddisfano la condizione di non negatività delle QUOTE DI CAPITALE e, quindi, il Prof. CARLO MARI dimostra matematicamente che sussiste nei c.d. “PAST AMASES” l’ANATOCISMO o COMPOSIZIONE DEGLI INTERESSI SUGLI INTERESSI..
Si allega anche la slide del Prof. CARLO MARI denominata “AMMORTAMENTI IN INTERESSE COMPOSTO E IN INTERESSE SEMPLICE: QUANDO «LA REALTÀ NON È COME CI APPARE»” del convegno di Civitavecchia del 30/05/2024 dove, rispetto alla slide denominata la “MATEMATICA VIOLATA”, si evidenzia ulteriormente sia che vi è corrispondenza nel REGIME COMPOSTO e nel REGIME SEMPLICE fra gli INTERESSI MATURATI in ogni periodo con gli INTERESSI PAGATI della rata corrispondente sia che LA COMPONENTE CAPITALE DEL PIANO DI AMMORTAMENTO SIA DEL REGIME COMPOSTO SIA DEL REGIME SEMPLICE È UNA MISCELA DI INTERESSI E CAPITALE. Non solo, nella slide del Prof. CARLO MARI del convegno di Civitavecchia del 30/05/2024 si mostra con ESEMPI NUMERICI sia gli interessi sugli interessi negli ammortamenti in REGIME COMPOSTO a rata costante (AMMORTAMENTO FRANCESE) o con quote di capitale costanti (AMMORTAMENTO ITALIANO) sia l’assenza degli interessi sugli interessi negli ammortamenti in REGIME SEMPLICE con impostazione iniziale in t_0 a rata costante (si rinvia all’articolo SOLO IL REGIME SEMPLICE CON IMPOSTAZIONE INIZIALE IN t_0 CON LA PONDERAZIONE DEI PERIODI RATEALI DELL’ANNO CIVILE CORRETTO RISPETTA AD OGNI ISTANTE TEMPORALE L’ART. 821, COMMA 3, CODICE CIVILE del 22 novembre 2022) o con quote di capitale costanti (si rinvia all’articolo VERITÀ MATEMATICHE INCONTROVERTIBILI: L’AMMORTAMENTO ITALIANO È DETERMINATO DAGLI INTERMEDIARI NEL REGIME COMPOSTO del 24 marzo 2020).
Nel rinviare all’articolo È INEQUIVOCABILE CHE L’ART. 821 C.C. PRESCRIVE L’UTILIZZO DELLA FORMULA DEL PRINCIPIO DI EQUITÀ DEL REGIME SEMPLICE DELLA RATA COSTANTE POSTICIPATA e all’articolo CASSA E DEPOSITI E PRESTITI EROGA FINANZIAMENTI RATEALI AGLI ENTI LOCALI NELL’ILLECITO REGIME COMPOSTO DEL SISTEMA ITALIANO (TASSO VARIABILE), in considerazione che CASSA DEPOSITI E PRESTITI nel PRESTITO ORDINARIO ENTI LOCALI prevede che in quello “a TASSO VARIABILE, il rimborso avviene in rate con quota capitale costante (metodo ITALIANO)”, di seguito si propone un esempio empirico che dimostra AGEVOLMENTE che il sistema dell’ammortamento ITALIANO è nel REGIME COMPOSTO degli interessi.
Le regole matematiche dell’ammortamento ITALIANO presenti nei manuali storici sono le seguenti:
a) QUOTE CAPITALI COSTANTI determinate dividendo la SOMMA EROGATA per il NUMERO delle RATE;
b) QUOTE INTERESSE posticipate determinate attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e il tasso effettivo annuo (o il tasso periodale effettivo o il tasso periodale NON equivalente perché semplicemente determinato dividendo il TAN per il tipo di periodicità adottato) con la formula I*DR.
A seguire un esempio che calcola con le regole matematiche storiche 24 RATE VARIABILI ANNUALI con la ponderazione dei periodi rateali dell’ANNO COMMERCIALE che ha una SOMMA EROGATA di euro 100.000,00 e un TASSO ANNUO del 5,00%.
Questo esempio di ammortamento ITALIANO che calcola le QUOTE INTERESSE posticipate attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e il TASSO ANNUO del 5,00% con la formula I*DR evidenzia l’inequivocabilità del REGIME ANATOCISTICO degli interessi perché, da una parte, la sommatoria delle rate attualizzate al TASSO ANNUO del 5,00% con la formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME COMPOSTO è pari alla Somma Erogata in t_0 di euro 100.000,00 e, dall’altra, la sommatoria dei montanti al TASSO ANNUO del 5,00% con la formula del PRINCIPIO DI EQUITÀ con impostazione finale in t_m del REGIME COMPOSTO è pari alla Somma Erogata in t_m del REGIME COMPOSTO al TASSO ANNUO del 5,00% di euro 322.509,99. Questa simmetria tra l’impostazione iniziale in t_0 e l’impostazione finale in t_m è la conseguenza del PRINCIPIO DI SCINDIBILITÀ che è una proprietà matematica peculiare del REGIME COMPOSTO, che nel nostro caso, garantisce 24 RATE VARIABILI ANNUALI identiche.
Invece, la sommatoria delle rate attualizzate con la formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE al TASSO ANNUO del 5,00% è pari a euro 109.892,00 e, quindi, essendo un valore diverso rispetto alla Somma Erogata in t_0 di euro 100.000,00, vi è prova matematica inequivocabile che il sistema dell’ammortamento ITALIANO è nel REGIME COMPOSTO degli interessi. Infatti, con l’importo di queste 24 RATE VARIABILI ANNUALI che comportano la restituzione complessiva di 62.500,00 euro di interessi corrispettivi, per ottenere la sommatoria delle rate attualizzate uguale alla Somma Erogata in t_0 di euro 100.000,00 con la formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE occorre utilizzare il TASSO ANNUO del 6,7397710024454%.
Ancora, la sommatoria dei montanti con la formula del PRINCIPIO DI EQUITÀ con impostazione finale in t_m del REGIME SEMPLICE al TASSO ANNUO del 5,00% è pari a euro 267.916,67 e, quindi, essendo un valore diverso rispetto alla Somma Erogata in t_m del REGIME SEMPLICE al TASSO ANNUO del 5,00% di euro 220.000,00, vi è prova matematica inequivocabile che il sistema dell’ammortamento ITALIANO è nel REGIME COMPOSTO degli interessi. Infatti, con l’importo di queste 24 RATE VARIABILI ANNUALI che comportano la restituzione complessiva di 62.500,00 euro di interessi corrispettivi, per ottenere la sommatoria dei montanti identica alla Somma Erogata in t_m del REGIME SEMPLICE occorre impiegare il TASSO ANNUO del 21,428573387754%. In altre parole, la Somma Erogata in t_0 di euro 100.000,00 ha una Somma Erogata in t_m del REGIME SEMPLICE di euro 614.285,76 e, questo importo, è identico alla sommatoria dei montanti delle 24 RATE VARIABILI ANNUALI che comportano la restituzione complessiva di 62.500,00 euro di interessi corrispettivi, solo se si impiega il TASSO ANNUO del 21,428573387754%.
Ovviamente, se un intermediario, come CASSA DEPOSITI E PRESTITI, applica l’ammortamento ITALIANO con la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e il tasso effettivo annuo (o il tasso periodale effettivo o il tasso periodale NON equivalente perché semplicemente determinato dividendo il TAN per il tipo di periodicità adottato) con la formula I*DR, viola l’art. 821, comma 3, c.c. perché questa norma mai derogata vieta il REGIME COMPOSTO che ha insito l’ANATOCISMO di TIPO GENETICO.
Non solo, se sono violate anche le disposizioni della Banca d’Italia previste con il PROTOTIPO FOGLIO INFORMATIVO che stabiliscono che “(5) Se nel piano di ammortamento si applica il regime di capitalizzazione composta degli interessi, la conversione del tasso di interesse annuale i1 nel corrispondente tasso di interesse infrannuale i2 (e viceversa) segue la seguente formula di equivalenza intertemporale i2 = (1+i1)t1/t2 – 1“ illustrata dettagliatamente nell’articolo PRINCIPIO DI EQUIVALENZA E PONDERAZIONI DEI PERIODI RATEALI, il contratto deve indicare anche il TASSO ANNUO EFFETTIVO (TAN REALE SOLO AMMORTAMENTO o TAN REALE FINANZIAMENTO se vi è un periodo di preammortamento), altrimenti sussiste l’INDETERMINATEZZA IN COMPOSTO del tasso corrispettivo.
AMMORTAMENTO ITALIANO del REGIME SEMPLICE con impostazione iniziale in t_0
Nel rinviare all’articolo SOLO IL REGIME SEMPLICE CON IMPOSTAZIONE INIZIALE IN t_0 CON LA PONDERAZIONE DEI PERIODI RATEALI DELL’ANNO CIVILE CORRETTO RISPETTA AD OGNI ISTANTE TEMPORALE L’ART. 821, COMMA 3, CODICE CIVILE, si può determinare un ammortamento ITALIANO del REGIME SEMPLICE con impostazione iniziale in t_0 utilizzando il PRINCIPIO DI SCINDIBILITÀ del BONFERRONI illustrato alla pagina 317 del manuale che deve essere impiegato per il calcolo delle QUOTE INTERESSI, modalità matematica che consente di precisare degli importi delle RATE VARIABILI che rispettano il PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE.
In questo caso, le regole matematiche imposte sono le seguenti:
a) QUOTE CAPITALI COSTANTI determinate dividendo la SOMMA EROGATA per il NUMERO delle RATE;
b) QUOTE INTERESSE posticipate determinate attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e il TASSO ANNUO (o il TASSO PERIODALE) determinato con la seguente formula
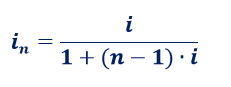
Di seguito l’esempio che calcola con le coordinate matematiche appena descritte 24 RATE VARIABILI ANNUALI con la ponderazione dei periodi rateali dell’ANNO COMMERCIALE che ha una SOMMA EROGATA di euro 100.000,00 e un TASSO ANNUO del 5,00%.
Questo esempio di ammortamento ITALIANO del REGIME SEMPLICE con impostazione iniziale in t_0 che calcola le QUOTE INTERESSE posticipate attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e la successione di TASSI ANNUI derivanti dall’utilizzo del PRINCIPIO DI SCINDIBILITÀ del BONFERRONI, cioè l’applicazione della formula sopracitata al TASSO ANNUO del 5,00%, evidenzia l’inequivocabilità del REGIME LINEARE degli interessi sia perché la sommatoria delle rate attualizzate con la formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE al TASSO ANNUO del 5,00% è pari alla Somma Erogata in t_0 di euro 100.000,00 sia perché, invece, la sommatoria delle rate attualizzate con la formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME COMPOSTO al TASSO ANNUO del 5,00% è pari a euro 91.153,71 e, quindi, è un valore diverso rispetto alla Somma Erogata in t_0 di euro 100.000,00. Infatti, con l’importo di queste 24 RATE VARIABILI ANNUALI che comportano la restituzione complessiva di 47.080,81 euro di interessi corrispettivi, per ottenere la sommatoria delle rate attualizzate uguale alla Somma Erogata in t_0 di euro 100.000,00 con la formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME COMPOSTO occorre utilizzare il TASSO ANNUO del 3,920787187108%.
AMMORTAMENTO ITALIANO del REGIME SEMPLICE con impostazione finale in t_m
Nel rinviare all’articolo EVIDENZIAZIONE MATEMATICA EMPIRICA DEL PERCHÈ IL REGIME SEMPLICE CON IMPOSTAZIONE FINALE IN t_m NON È COERENTE AD OGNI ISTANTE TEMPORALE AL VALORE DEL MONTANTE DEL REGIME SEMPLICE, si può determinare un ammortamento ITALIANO del REGIME SEMPLICE con impostazione finale in t_m utilizzando la logica matematica del PRINCIPIO DI SCINDIBILITÀ del BONFERRONI illustrato alla pagina 317 del manuale che deve essere impiegato per il calcolo delle QUOTE INTERESSI, modalità matematica che consente di precisare degli importi delle RATE VARIABILI che rispettano il PRINCIPIO DI EQUITÀ con impostazione finale in t_m del REGIME SEMPLICE.
In questo caso, le regole matematiche imposte sono le seguenti:
a) QUOTE CAPITALI COSTANTI determinate dividendo la SOMMA EROGATA per il NUMERO delle RATE;
b) QUOTE INTERESSE posticipate determinate attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e il TASSO ANNUO (o il TASSO PERIODALE) determinato con la seguente formula
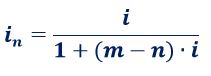
Di seguito l’esempio che calcola con le coordinate matematiche appena descritte 24 RATE VARIABILI ANNUALI con la ponderazione dei periodi rateali dell’ANNO COMMERCIALE che ha una SOMMA EROGATA di euro 100.000,00 e un TASSO ANNUO del 5,00%.
Questo esempio di ammortamento ITALIANO del REGIME SEMPLICE con impostazione finale in t_m che calcola le QUOTE INTERESSE posticipate attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e la successione di TASSI ANNUI derivanti dall’utilizzo del PRINCIPIO DI SCINDIBILITÀ del BONFERRONI, cioè l’applicazione della formula sopracitata al TASSO ANNUO del 5,00%, evidenzia l’inequivocabilità del REGIME LINEARE degli interessi sia perché la sommatoria dei montanti con la formula del PRINCIPIO DI EQUITÀ con impostazione finale in t_m del REGIME SEMPLICE al TASSO ANNUO del 5,00% è pari alla Somma Erogata in t_m del REGIME SEMPLICE al TASSO ANNUO del 5,00% di euro 220.000,00.
Inoltre, l’ulteriore prova matematica inequivocabile che questo esempio di ammortamento ITALIANO del REGIME SEMPLICE con impostazione finale in t_m è nel REGIME LINEARE degli interessi è dato dal fatto che la sommatoria dei montanti con la formula del PRINCIPIO DI EQUITÀ con impostazione finale in t_m del REGIME COMPOSTO al TASSO ANNUO del 5,00% è pari a euro 261.719,43 e, quindi, è un valore diverso rispetto alla Somma Erogata in t_m del REGIME COMPOSTO al TASSO ANNUO del 5,00% di euro 322.509,99.
Infatti, con l’importo di queste 24 RATE VARIABILI ANNUALI che comportano la restituzione complessiva di 36.487,83 euro di interessi corrispettivi, per ottenere la sommatoria dei montanti identica alla Somma Erogata in t_m del REGIME COMPOSTO occorre impiegare il TASSO ANNUO del 2,836753684087%. In altre parole, la Somma Erogata in t_0 di euro 100.000,00 ha una Somma Erogata in t_m del REGIME COMPOSTO di euro 195.686,38 e, questo importo, è identico alla sommatoria dei montanti delle 24 RATE VARIABILI ANNUALI che comportano la restituzione complessiva di 36.487,83 euro di interessi corrispettivi, solo se si impiega il TASSO ANNUO del 2,836753684087%.
In conclusione, speriamo che gli avvocati non propongano più come alternativa del sistema FRANCESE il sistema ITALIANO determinato attraverso la moltiplicazione fra il DEBITO RESIDUO dell’istante precedente al rimborso e il tasso effettivo annuo (o il tasso periodale effettivo o il tasso periodale NON equivalente perché semplicemente determinato dividendo il TAN per il tipo di periodicità adottato) con la formula I*DR perché lo stesso è precisato inequivocabilmente nel illecito REGIME COMPOSTO degli interessi in violazione dell’art. 821, comma 3, c.c..
VOLUME I sul portale www.youcanprint.it

In particolare, vi è tutta la costruzione matematica INEDITA di DEVIS ABRIANI sulle diverse ponderazioni dei periodi rateali (Anno Civile Corretto (365/365 e 366/366), Anno Civile Non Corretto (365/365 e 366/365), Anno Misto (365/360 e 366/360), Anno Commerciale (360/360) del Montante in Semplice e Composto, della rata costante posticipata (Francese) in Semplice (in t_0 e in t_m) e Composto (in t_0 e in t_m) e della rata variabile posticipata (Italiano) in Semplice (in t_0 e in t_m) e Composto (in t_0 e in t_m)
VOLUME II sul portale www.youcanprint.it

In particolare, si illustra: a) l’obbligo giuridico dell’uso della ponderazione dei periodi rateali dell’anno civile corretto spiegata da Devis Abriani nel VOLUME 1 PRINCIPI DI MATEMATICA FINANZIARIA BASILARI PER COMPRENDERE I FINANZIAMENTI RATEALI; b) la prova matematica/empirica che il Regime Composto (“Francese” o “Italiano”) è illecito ex art. 821 c.c.; c) la prova matematica/empirica che unicamente il Regime Semplice con impostazione iniziale in t_0 (“Francese” o “Italiano”) rispetta ad ogni istante temporale l’art. 821 c.c.; d) la prova matematica/empirica che il Regime Semplice con impostazione finale in t_m (“Francese” o “Italiano”) NON rispetta ad ogni istante temporale l’art. 821 c.c.; e) la modalità matematica/empirica corretta giuridicamente per il calcolo della Tentata Truffa e della Truffa Consumata; f) la modalità matematica/empirica corretta giuridicamente per il calcolo della Tentata Truffa Attualizzata da utilizzare per la verifica dell’Usurarietà del contratto; g) la prova matematica/empirica dell’impossibilità di determinazione dell’aliquota dell’indeterminatezza contrattuale del tasso corrispettivo se si usa il Regime Semplice con impostazione finale in t_m a causa dell’asintoto verticale; h) la prova matematica/empirica dei reati di Truffa e Autoriciclaggio di Cassa Depositi Prestiti per i finanziamenti concessi agli Enti locali.
