
ABSTRACT
In primis, questo articolo può essere compreso compiutamente da un punto di vista matematico se si ha presente che sia nel REGIME COMPOSTO sia nel REGIME SEMPLICE, da una parte, il conseguenziale PIANO DI AMMORTAMENTO (o PIANO DI RIMBORSO) è univocamente determinato nei suoi valori numerici dall’impiego nella 1° fase algebrica dell’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 o con impostazione finale in t_m che determina l’importo della rata costante posticipata e, dall’altra parte, che il DEBITO RESIDUO del PIANO DI AMMORTAMENTO (o PIANO DI RIMBORSO) è un MONTANTE e, quindi, una miscela di CAPITALE e INTERESSE (si rinvia all’articolo PROF. FRANCESCO SOAVE (LUGANO 1743 – PAVIA 1806) del 23 marzo 2020, all’articolo PROF. A. CASANO DEL 1800 del 24 marzo 2020, all’articolo BONFERRONI 1937 IL PRINCIPIO DI EQUITÀ E IL PIANO DI AMMORTAMENTO SONO LE 2 FASI MATEMATICHE DELLA STESSA MEDAGLIA del 23 marzo 2020 , all’articolo BONFERRONI 1937 IL PRINCIPIO DI EQUITÀ DETERMINA GLI INTERESSI EFFETTIVI del 23 marzo 2020, all’articolo BONFERRONI 1937 IL PIANO DI AMMORTAMENTO LINEARE DELLA RATA CALCOLATA CON IL PRINCIPIO DI EQUITÀ DEL REGIME SEMPLICE CON IMPOSTAZIONE INIZIALE IN t_0 del 23 marzo 2020, all’articolo LEVI 1953 CAPITALIZZAZIONE E SUO SIGNIFICATO del 23 marzo 2020, all’articolo LEVI 1953-1959 VINCOLO EPOCA DI RIFERIMENTO del 23 marzo 2020, all’articolo LEVI 1964 PRINCIPIO DI SCINDIBILITÀ del 23 marzo 2020, all’articolo BONFERRONI 1937, PIANO DI AMMORTAMENTO DELLA RATA COSTANTE POSTICIPATA CALCOLATA CON IL PRINCIPIO DI EQUITÀ DEL REGIME SEMPLICE CON IMPOSTAZIONE FINALE IN t_m del 25 marzo 2021, all’articolo VAROLI 1983, PIANO DI AMMORTAMENTO DELLA RATA COSTANTE POSTICIPATA CALCOLATA CON IL PRINCIPIO DI EQUITÀ DEL REGIME SEMPLICE CON IMPOSTAZIONE FINALE IN t_m del 26 marzo 2020, all’articolo BONFERRONI 1937, TASSO NOMINALE, TASSI TECNICI, TASSO EFFETTIVO O REALE del 25 marzo 2020 e all’articolo RIVISTA ASSOBANK BANCHE&BANCHIERI 2/2015 del 23 marzo 2020, all’articolo MORICONI 1994 IL PIANO DI AMMORTAMENTO FRANCESE DELLA RATA CALCOLATA CON IL PRINCIPIO DI EQUITÀ DEL REGIME COMPOSTO SI DETERMINA PRIORITARIAMENTE CON “A FIGURATO M AL TASSO I” del 06 agosto 2020, all’articolo LA COMPONENTE CAPITALE DEL PIANO DI AMMORTAMENTO SIA DEL REGIME COMPOSTO SIA DEL REGIME SEMPLICE È UNA MISCELA DI INTERESSI E CAPITALE 20 gennaio 2023).
In particolare, nel rinviare all’articolo LA COMPONENTE CAPITALE DEL PIANO DI AMMORTAMENTO SIA DEL REGIME COMPOSTO SIA DEL REGIME SEMPLICE È UNA MISCELA DI INTERESSI E CAPITALE 20 gennaio 2023, per comprendere in sintesi perché da un punto di vista matematico NEI PRESTITI GRADUALI DELLA RATA COSTANTE POSTICIPATA GLI INTERESSI NON SONO ESIGIBILI (PAGATI) PRIMA DELLA LORO MATURAZIONE basta leggere quanto afferma il Prof. CARLO MARI nel saggio Sulla modellizzazione dei prestiti: errori, nonsense e mistificazioni nello scritto di F. Cacciafesta: “Facciamo notare che il DEBITO RESIDUO è una MISCELA di capitale e interessi non solo nel REGIME DELL’INTERESSE COMPOSTO ma in qualunque altro regime, anche in INTERESSE SEMPLICE. … (…) … Gli interessi maturati e non corrisposti restano all’interno del DEBITO RESIDUO a comporre quella MISCELA di capitale e interessi … (…) … È questo un punto cruciale della trattazione perché consente di dimostrare agevolmente la presenza di interessi generati da interessi negli ammortamenti in REGIME COMPOSTO.”
Si allega la slide del Prof. CARLO MARI denominata la “MATEMATICA VIOLATA” pubblicata sul sito della Cassazione del Convegno 31 gennaio 2024 : Mutuo bancario con ammortamento alla francese che analizza compiutamente l’impianto teorico di base della matematica finanziaria così come espresso nei manuali sia del Prof. ALESSANDRO CASANO (Elementi di Algebra, Palermo, 1845) sia del Prof. GIUSEPPE OTTAVIANI (Lezioni di Matematica Finanziaria, Veschi, Milano, 1988) contestando apertamente la conclusione più rilevante di tutto il rapporto AMASES di pagina 21 che afferma che “se vale la regola di calcolo degli interessi su espressa (formalizzata nella Reg. 1 del rapporto a pagina 17), una sequenza input di quote capitale tutte positive (o almeno non negative) è garanzia di assenza di interessi su interessi in ogni stadio del PAST“.
In altre parole, la slide del Prof. CARLO MARI dimostra la balla matematica che i c.d. “PAST AMASES” a rata costante (AMMORTAMENTO FRANCESE) e i c.d. “PAST AMASES” con quote di capitale costanti (AMMORTAMENTO ITALIANO) soddisfano la condizione di non negatività delle QUOTE DI CAPITALE e, quindi, il Prof. CARLO MARI dimostra matematicamente che sussiste nei c.d. “PAST AMASES” l’ANATOCISMO o COMPOSIZIONE DEGLI INTERESSI SUGLI INTERESSI.
Si allega anche la slide del Prof. CARLO MARI denominata “AMMORTAMENTI IN INTERESSE COMPOSTO E IN INTERESSE SEMPLICE: QUANDO «LA REALTÀ NON È COME CI APPARE»” del convegno di Civitavecchia del 30/05/2024 dove, rispetto alla slide denominata la “MATEMATICA VIOLATA”, si evidenzia ulteriormente sia che vi è corrispondenza nel REGIME COMPOSTO e nel REGIME SEMPLICE fra gli INTERESSI MATURATI in ogni periodo con gli INTERESSI PAGATI della rata corrispondente sia che LA COMPONENTE CAPITALE DEL PIANO DI AMMORTAMENTO SIA DEL REGIME COMPOSTO SIA DEL REGIME SEMPLICE È UNA MISCELA DI INTERESSI E CAPITALE. Non solo, nella slide del Prof. CARLO MARI del convegno di Civitavecchia del 30/05/2024 si mostra con ESEMPI NUMERICI sia gli interessi sugli interessi negli ammortamenti in REGIME COMPOSTO a rata costante (AMMORTAMENTO FRANCESE) o con quote di capitale costanti (AMMORTAMENTO ITALIANO) sia l’assenza degli interessi sugli interessi negli ammortamenti in REGIME SEMPLICE con impostazione iniziale in t_0 a rata costante (si rinvia all’articolo SOLO IL REGIME SEMPLICE CON IMPOSTAZIONE INIZIALE IN t_0 CON LA PONDERAZIONE DEI PERIODI RATEALI DELL’ANNO CIVILE CORRETTO RISPETTA AD OGNI ISTANTE TEMPORALE L’ART. 821, COMMA 3, CODICE CIVILE del 22 novembre 2022) o con quote di capitale costanti (si rinvia all’articolo VERITÀ MATEMATICHE INCONTROVERTIBILI: L’AMMORTAMENTO ITALIANO È DETERMINATO DAGLI INTERMEDIARI NEL REGIME COMPOSTO del 24 marzo 2020).
In particolare, ecco come la slide del Prof. CARLO MARI denominata “AMMORTAMENTI IN INTERESSE COMPOSTO E IN INTERESSE SEMPLICE: QUANDO «LA REALTÀ NON È COME CI APPARE»” del convegno di Civitavecchia del 30/05/2024 sintetizza che vi è corrispondenza nel REGIME COMPOSTO e nel REGIME SEMPLICE fra gli INTERESSI MATURATI in ogni periodo con gli INTERESSI PAGATI della rata corrispondente

ARTICOLO
Si legge nell’ordinanza interlocutoria della Corte di Cassazione del 24/05/2021 n. 14166 che “12. – Con riferimento al primo motivo di ricorso, si deve osservare che il tema, così specificamente proposto all’esame, viene a concentrarsi sull’interpretazione da assegnare all’espressione “interessi dovuti”, che è contenuta nella norma dell’art. 2855 c.c., comma 2. In particolare, se tale formula rinvii agli interessi divenuti esigibili (ovvero scaduti), stando a quanto stabilito dal piano di ammortamento pattuito, nelle due annate anteriori a quella in cui è caduta la sentenza dichiarativa del fallimento, secondo quanto ritenuto dal decreto del Tribunale trevigiano; o se, invece, rinvii agli interessi che siano anche (e anzi, a ben vedere, prima di tutto) maturati nel corso di tale periodo di tempo, come per contro viene affermato dal ricorrente. Il divario che può effettivamente intercorrere tra le opzioni interpretative appena segnalate – va subito messo in chiaro – emerge, e si apprezza, in ragione del fatto che, secondo quanto incontestato in causa, i due contratti di mutuo hanno predisposto un piano di rientro dell’erogato, che risulta articolato secondo il SISTEMA DELL’AMMORTAMENTO “ALLA FRANCESE.”
L’ordinanza interlocutoria della Corte di Cassazione del 24/05/2021 n. 14166 prosegue affermando che “13. – La struttura di questo tipo di ammortamento prevede come ha per l’appunto rilevato il Tribunale – che lo stesso sia composto da quote di (restituzione del) capitale e quote di (pagamento degli) interessi compensativi “in rapporto variabile nella successione delle rate”: e così a muovere, più precisamente, dalle rate iniziali, in cui la misura assegnata agli interessi è preponderante, e comunque superiore, rispetto a quella che viene imputata al capitale ancora da restituire; secondo una dinamica in via progressiva decrescente col susseguirsi delle rate; sino a invertire il rapporto quantitativo tra le quote di interessi e di capitale nelle rate inerenti alla fase terminale del previsto rientro. Ne segue che detto tipo di ammortamento comporta – per propria conformazione strutturale, seppur con intensità maggiore o minore a seconda delle fattispecie che nel concreto lo realizzino – che una parte degli interessi posti a remunerazione del mutuo erogato divengano esigibili prima che siano maturati, per maturare in epoca successiva alla scadenza fissata per relativo pagamento. Secondo il principio espresso nell’art. 820 c.c., (comma 3), e nell’art. 821 c.c., (comma 3), infatti, gli interessi – quali frutti civili del capitale dato in “godimento” “si acquistano”, e cioè maturano, “giorno per giorno, in ragione della durata del diritto.”
Preliminarmente, l’ordinanza interlocutoria della Corte di Cassazione del 24/05/2021 n. 14166 dimostra di NON avere contezza delle regole matematiche quando afferma che nel “SISTEMA DELL’AMMORTAMENTO “ALLA FRANCESE” … (…) … una parte degli interessi posti a remunerazione del mutuo erogato divengano esigibili prima che siano maturati, per maturare in epoca successiva alla scadenza fissata per relativo pagamento“. Infatti, dato che nel REGIME COMPOSTO il conseguenziale PIANO DI AMMORTAMENTO FRANCESE è univocamente determinato nei suoi valori numerici dall’impiego nella 1° fase algebrica dell’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 o con impostazione finale in t_m che precisa l’importo della rata costante posticipata, ad ogni pagamento di rata l’intermediario incassa (esige) SOLO degli interessi corrispettivi maturati matematicamente in quell’istante temporale e, quindi, NON sussiste un pagamento ANTICIPATO di interessi corrispettivi che maturano in un “epoca successiva alla scadenza.”
Non solo, anche nell’eventualità che nella 1° fase algebrica fosse utilizzata l’equazione del PRINCIPIO DI EQUITÀ del REGIME SEMPLICE con impostazione iniziale in t_0 o con impostazione finale in t_m allo scopo di determinare l’importo della rata costante posticipata, l’intermediario incasserebbe (esigerebbe) solo degli interessi corrispettivi maturati matematicamente in quell’istante temporale perché il conseguenziale PIANO DI AMMORTAMENTO LINEARE è univocamente determinato nei suoi valori numerici.
In altre parole, sia nel REGIME COMPOSTO del sistema FRANCESE sia nel REGIME SEMPLICE del sistema LINEARE, gli importi numerici del conseguenziale PIANO DI AMMORTAMENTO, che evidenziano in entrambi i regimi degli interessi, all’inizio del rimborso, una sequenza di QUOTE CAPITALE variabili con valori di importo inferiore rispetto a quelli della sequela di QUOTE INTERESSE mentre, alla fine del rimborso, si realizza esattamente il fenomeno algebrico contrario, sono dei dati numerici con una sequenza algebrica predefinita dall’equazione del PRINCIPIO DI EQUITÀ che ESCLUDE da un punto di vista matematico che si hanno ad ogni pagamento di rata delle QUOTE INTERESSE che maturano “in epoca successiva alla scadenza fissata per relativo pagamento“. Ulteriormente, si segnala che le evidenze numeriche con questa sequela matematica predefinita dall’equazione del PRINCIPIO DI EQUITÀ, sequenza che si realizza identicamente sia del PIANO DI AMMORTAMENTO del sistema FRANCESE sia del PIANO DI AMMORTAMENTO del sistema LINEARE, sono rispettose dell’art. 1194 c.c. che stabilisce che “Il debitore non può imputare il pagamento al capitale, piuttosto che agli interessi e alle spese, senza il consenso del creditore. Il pagamento fatto in conto di capitale e d’interessi deve essere imputato prima agli interessi.”
Conseguentemente, è errato sia da un punto di vista matematico sia da un punto di vista logico giuridico il richiamo nell’ordinanza interlocutoria della Corte di Cassazione del 24/05/2021 n. 14166 del “principio espresso nell’art. 820 c.c., (comma 3), e nell’art. 821 c.c., (comma 3)” allo scopo di giustificare l’affermazione che nel PIANO DI AMMORTAMENTO del sistema FRANCESE, dato che vi è la sequenza matematica predefinita dall’equazione del PRINCIPIO DI EQUITÀ descritta in precedenza, vi sono delle QUOTE INTERESSE che maturano “in epoca successiva alla scadenza fissata per relativo pagamento.”
Infatti, il combinato disposto che “gli interessi – quali frutti civili del capitale dato in “godimento” “si acquistano”, e cioè maturano, “giorno per giorno, in ragione della durata del diritto” rileva solo per sancire sia che il principio di proporzionalità ex art. 821, comma 3, c.c. deve sussistere ad ogni pagamento di rata, sia che nei prestiti graduali deve essere impiegata obbligatoriamente l’equazione del PRINCIPIO DI EQUITÀ del REGIME SEMPLICE con impostazione iniziale in t_0 per determinare nella 1° fase algebrica l’importo della rata costante posticipata come illustrato nell’articolo SOLO IL REGIME SEMPLICE CON IMPOSTAZIONE INIZIALE IN t_0 CON LA PONDERAZIONE DEI PERIODI RATEALI DELL’ANNO CIVILE CORRETTO RISPETTA AD OGNI ISTANTE TEMPORALE L’ART. 821, COMMA 3, CODICE CIVILE del 22 novembre 2022.
Nel rinviare all’articolo IL BULLET È ANATOCISTICO del 24 marzo 2020, all’articolo LA MOLTIPLICAZIONE FRA IL TASSO E IL DEBITO RESIDUO DEL SISTEMA FRANCESE È NEL REGIME COMPOSTO ANCHE NEL PREAMMORTAMENTO DOVE LE QUOTE CAPITALI SONO PARI A ZERO del 17 maggio 2021 e all’articolo È INEQUIVOCABILE CHE L’ART. 821 C.C. PRESCRIVE L’UTILIZZO DELLA FORMULA DEL PRINCIPIO DI EQUITÀ DEL REGIME SEMPLICE DELLA RATA COSTANTE POSTICIPATA del 21 marzo 2020, si presenta un esempio empirico (SOMMA EROGATA euro 1.000,00 da rimborsare in 4 rate costanti posticipate annuali al tasso annuo del 10,00%) che dimostra che si dichiara il FALSO matematico quando si afferma che il sistema “FRANCESE” ha una rata costante posticipata determinata con il PRINCIPIO DI EQUITÀ del REGIME COMPOSTO (1° FASE) e il suo conseguenziale piano di ammortamento (2° FASE), anziché essere inequivocabilmente nel REGIME ANATOCISTICO, è un “separato conteggio” in REGIME SEMPLICE.
Ulteriormente, nel rinviare all’articolo I REQUISITI E I CRITERI DI IDONEITÀ DEI BANCARI LATU SENSU PROVANO IL DOLO NEI REATI CONSEGUENTI ALL’IMPIEGO DEL SISTEMA FRANCESE del 26 ottobre 2020 e all’articolo SANZIONE EX OFFICIO EX ART. 96, COMMA 3, C.P.C. del 11 aprile 2022, si evidenzia che i bancari latu sensu, dotati della diligenza qualificata del BONUS ARGENTARIUS ex art. 1176, comma 2, c.c., e i loro matematici, determinano commercialmente la rata costante posticipata con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME COMPOSTO sia con la ponderazione dei periodi rateali dell’ANNO CIVILE “NON CORRETTO” e i vari e diversi tassi NON equivalenti periodali conseguenti ai fattori positivi di periodicità q_k non identici delle scale temporali diverse da quella giornaliera (si rinvia all’articolo GLI INTERMEDIARI CON IL SISTEMA FRANCESE USANO LE PONDERAZIONI DEI PERIODI RATEALI DIVERSE DA QUELLA DELL’ANNO COMMERCIALE del 09 maggio 2021) sia con la ponderazione dei periodi rateali dell’ANNO “MISTO” (365/360 e 366/360) e i vari e diversi tassi NON equivalenti periodali conseguenti ai fattori positivi di periodicità q_k non identici delle scale temporali diverse da quella giornaliera (si rinvia all’articolo GLI INTERMEDIARI NEI PRESTITI RATEALI A TASSO VARIABILE EROGATI CON IL SISTEMA FRANCESE MANIPOLANO LE REGOLE MATEMATICHE E CONTRATTUALI del 09 maggio 2021) sia con la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” ex art. 821, comma 3, c.c. ed ex Normativa di Trasparenza della Banca d’Italia e i vari e diversi tassi NON equivalenti periodali conseguenti ai fattori positivi di periodicità q_k non identici delle scale temporali diverse da quella giornaliera (si rinvia all’articolo GLI INTERMEDIARI CON IL SISTEMA FRANCESE CONOSCONO PERFETTAMENTE LE REGOLE MATEMATICHE E GIURIDICHE: LA PONDERAZIONE DEI PERIODI RATEALI DELL’ANNO CIVILE CORRETTO CON I VARI TASSI PERIODALI NON EQUIVALENTI NEL REGIME COMPOSTO del 06 luglio 2022).
Di seguito un altro esempio empirico che dimostra che si dichiara il FALSO matematico quando si afferma che il sistema “FRANCESE” ha una rata costante posticipata determinata con il PRINCIPIO DI EQUITÀ del REGIME COMPOSTO (1° FASE) e il suo conseguenziale piano di ammortamento (2° FASE), anziché essere inequivocabilmente nel REGIME ANATOCISTICO, è un “separato conteggio” in REGIME SEMPLICE perché, se si calcola il valore finanziario dell’operazione ad ogni pagamento di rata del sistema “FRANCESE” confrontandolo con il valore finanziario del MONTANTE del REGIME SEMPLICE di ogni pagamento, cioè l’unico valore che rispetta il principio di proporzionalità ex art. 821, comma 3, c.c., la rata costante posticipata determinata con il PRINCIPIO DI EQUITÀ del REGIME COMPOSTO (1° FASE) e il suo conseguenziale piano di ammortamento (2° FASE) sono inequivocabilmente nel REGIME ANATOCISTICO in quanto l’intermediario incassa maggiori INTERESSI CORRISPETTIVI. Conseguentemente, nel REGIME COMPOSTO NON vi sono delle QUOTE INTERESSE che maturano “in epoca successiva alla scadenza fissata per relativo pagamento.”
Al contrario, se si calcola il valore finanziario dell’operazione ad ogni pagamento di rata del sistema “LINEARE” con l’impostazione iniziale in t_0 confrontandolo con il valore finanziario del MONTANTE del REGIME SEMPLICE di ogni pagamento, cioè l’unico valore che rispetta il principio di proporzionalità, queste rate costanti posticipate determinate con l’impostazione iniziale in t_0 hanno un valore finanziario dell’operazione ad ogni pagamento di rata IDENTICO a quello previsto obbligatoriamente dall’art. 821, comma 3, codice civile. Conseguentemente, nel REGIME SEMPLICE con l’impostazione iniziale in t_0 NON vi sono delle QUOTE INTERESSE che maturano “in epoca successiva alla scadenza fissata per relativo pagamento.”
Si tratta di un piccolo esempio numerico di una Somma Erogata di euro 1.000,00 da rimborsare in 4 rate annuali posticipate al tasso annuo del 10,00% con la data di inizio ammortamento del 31/03/2011 usando sia la formula del REGIME COMPOSTO con impostazione iniziale in t_0 che impiega la ponderazione dei periodi rateale dell’ANNO “MISTO”
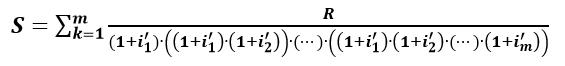
che determina con tali parametri la rata costante posticipata arrotondata del sistema “FRANCESE” di euro 316,50 sia la formula del REGIME COMPOSTO con impostazione iniziale in t_0 che utilizza la ponderazione dei periodi rateale dell’ANNO CIVILE “CORRETTO”
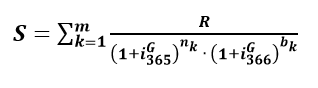
che precisa la rata costante posticipata arrotondata del sistema “FRANCESE” di euro 315,49 sia la formula del REGIME SEMPLICE con impostazione iniziale in t_0 che impiega la ponderazione dei periodi rateale dell’ANNO CIVILE “CORRETTO”
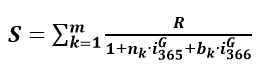
che determina la rata costante posticipata arrotondata del sistema “LINEARE” di euro 310,00.
Per essere più chiari, per confutare la giurisprudenza e la dottrina matematica che non evidenzia che è nella 1° Fase Matematica che si determinano gli INTERESSI EFFETTIVI CORRISPETTIVI sia con l’applicazione dell’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO con impostazione iniziale in t_0 sia con l’applicazione dell’equazione del PRINCIPIO DI EQUITÀ del REGIME SEMPLICE con impostazione iniziale in t_0 e, quindi, per contrastare la giurisprudenza e la dottrina matematica che non effettua la valutazione di congruità del quantitativo complessivo degli INTERESSI EFFETTIVI CORRISPETTIVI con riferimento al dettato normativo dell’art. 821, comma 3, c.c., si mette in risalto un esempio numerico di calcolo di SOLI interessi corrispettivi di PREAMMORTAMENTO che dimostra che qualsiasi moltiplicazione fra una somma e il tasso di interesse pattuito è effettuata nel REGIME COMPOSTO degli interessi se le rate sono più di una (Somma Erogata di euro 1.000,00; tasso annuo di preammortamento del 10,00%; pagamento di 4 rate annuali posticipate di soli interessi di preammortamento calcolate con la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” con la data di inizio preammortamento del 31/03/2011).
Si rinvia per ulteriori spiegazioni all’articolo LA MOLTIPLICAZIONE FRA IL TASSO E IL DEBITO RESIDUO DEL SISTEMA FRANCESE È NEL REGIME COMPOSTO ANCHE NEL PREAMMORTAMENTO DOVE LE QUOTE CAPITALI SONO PARI A ZERO del 17 maggio 2021.
VOLUME I sul portale www.youcanprint.it

In particolare, vi è tutta la costruzione matematica INEDITA di DEVIS ABRIANI sulle diverse ponderazioni dei periodi rateali (Anno Civile Corretto (365/365 e 366/366), Anno Civile Non Corretto (365/365 e 366/365), Anno Misto (365/360 e 366/360), Anno Commerciale (360/360) del Montante in Semplice e Composto, della rata costante posticipata (Francese) in Semplice (in t_0 e in t_m) e Composto (in t_0 e in t_m) e della rata variabile posticipata (Italiano) in Semplice (in t_0 e in t_m) e Composto (in t_0 e in t_m)
VOLUME II sul portale www.youcanprint.it

In particolare, si illustra: a) l’obbligo giuridico dell’uso della ponderazione dei periodi rateali dell’anno civile corretto spiegata da Devis Abriani nel VOLUME 1 PRINCIPI DI MATEMATICA FINANZIARIA BASILARI PER COMPRENDERE I FINANZIAMENTI RATEALI; b) la prova matematica/empirica che il Regime Composto (“Francese” o “Italiano”) è illecito ex art. 821 c.c.; c) la prova matematica/empirica che unicamente il Regime Semplice con impostazione iniziale in t_0 (“Francese” o “Italiano”) rispetta ad ogni istante temporale l’art. 821 c.c.; d) la prova matematica/empirica che il Regime Semplice con impostazione finale in t_m (“Francese” o “Italiano”) NON rispetta ad ogni istante temporale l’art. 821 c.c.; e) la modalità matematica/empirica corretta giuridicamente per il calcolo della Tentata Truffa e della Truffa Consumata; f) la modalità matematica/empirica corretta giuridicamente per il calcolo della Tentata Truffa Attualizzata da utilizzare per la verifica dell’Usurarietà del contratto; g) la prova matematica/empirica dell’impossibilità di determinazione dell’aliquota dell’indeterminatezza contrattuale del tasso corrispettivo se si usa il Regime Semplice con impostazione finale in t_m a causa dell’asintoto verticale; h) la prova matematica/empirica dei reati di Truffa e Autoriciclaggio di Cassa Depositi Prestiti per i finanziamenti concessi agli Enti locali.
PARAGRAFO 11 VOLUME II “Tasso corrispettivo: il reato-mezzo di Truffa aggravato ex art. 61, comma 1, n. 2, c.p. dalla connessione con il reato-fine di Usura nei contratti di finanziamento rateale. La problematica conseguenziale del reato societario di Autoriciclaggio e del reato di Estorsione”
